摘要：GM(1,1)模型是应用范围极广的灰指数模型，其精度取决于背景值的构造形式和初始条件的选取。在误差最小化准则下构建了基于粒子群算法的GM(1,1)模型，同时对模型的背景值系数和初始值进行了优化。运用优化的模型分别对齐次指数序列、2017—2021年我国新能源汽车保有量进行拟合。实例分析表明，基于粒子群算法优化的GM(1,1)模型适合中长期预测并且具有更高的拟合精度。

关键词：GM(1,1)模型；粒子群算法；背景值；初始条件；误差最小化

中图分类号：C931    文献标识码：B    文章编号：1671-2064(2023)13-0094-05

0 引言

灰色系统理论是由我国著名学者邓聚龙教授首创的一门系统科学理论，其产生与发展为人们科学认识和解决不确定的系统问题提供了一个新的视角^[1]。GM(1,1)模型作为经典的灰色预测模型，具有所需原始数据量少、计算简便、适用性强等优点，在农业、工业、经济管理、工程技术等领域中得到了广泛应用。然而传统GM(1,1)模型也存在一定的局限性，当发展系数越大时，GM(1,1)模型的预测精度越低。为提升传统GM(1,1)模型的精度，扩大适用范围，学者们进行了大量的研究，结果表明，模型背景值构造以及初始值选取极大程度上影响了预测精度。背景值优化方面，一是优化传统的背景值公式，如蒋诗泉^[2]利用复化梯形公式优化背景值，王晓佳等^[3]将分段线性插值函数与Newton插值公式相结合，改进了背景值的构造方法。背景值公式优化方法尽管在一定程度上提升了模型精度，但是背景值计算均较为复杂。基于此，张可^[4]结合非线性优化的粒子群算法对背景值参数直接进行寻优，提升了预测精度，扩大了模型使用范围；杨孝良^[5]提出三参数背景值构造的新方法，提升了背景值的平滑效果；徐宁^[6]基于误差最小化对GM(1,1)模型背景值进行优化，该方法改善了发展系数较大时建模精度低的不足，保持了较好的无偏性，计算过程也很简便，但是证明基于原始序列有齐次指数增长规律的前提，限制了模型的适用范围。初始条件优化方面，熊萍萍^[7]针对非等间距 GM(1,1) 模型的预测问题，提出以非等间距一阶累加生成序列各分量的加权平均数作为优化的初始值，通过算例验证了所提出的非等间距优化模型的有效性和可行性；张彬^[8]将背景值优化公式和边值修正相结合对模型进行改进；郑雪平^[9]借鉴徐宁和张彬的思路，将初值优化方法和背景值优化结合起来进行模型优化,使近似齐次指数序列拟合效果得到明显提升。

为提升模型的适应性，本文利用智能算法实现动态寻优的目的，采用平均相对误差最小准则，构建适应度函数，将传统GM(1,1)模型的背景值系数与初始条件同时优化后，运用粒子群算法得到最优值，通过算例对优化后GM(1,1)模型的适用范围和有效性进行了验证。

1 传统GM(1,1)模型

定义1  设原始非负序列，序列

的一阶累加序列，，其中，的紧邻均值生成序列，方程

（1）

称为GM(1,1)模型的定义式，z⁽¹⁾(k)称为GM(1,1)模型的背景值，a,b为待定系数。

令 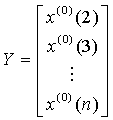 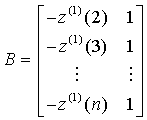，待定系数列[a,b]^T在最小二乘意义下的估计为：

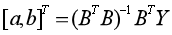（2）  

定义2 假设X^（0）为非负序列，X^（1）为X^（0）的一阶累加序列，a，b，B如定义1中所示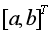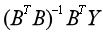， =，称方程

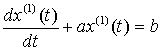（3）

为GM(1,1)模型对应的白化微分方程。

取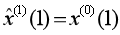为初始条件，将参数a，b代入微分方程求解，可得X^（1）的时间响应式为：

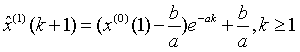（4）

将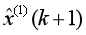序列进行累减，得到原始序列X^（0）的时间响应式为：

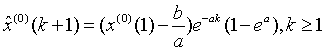（5）

-a，b分别称为发展系数与灰色作用量,-a反映了预测序列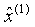和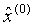的发展态势。上述建模过程可以看出GM(1,1)模型对原始序列实现预测分成两个主要步骤：（1）由原始序列生成一阶累加序列以及紧邻均值序列，通过定义式（1）利用最小二乘法估计出参数列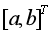；（2）将参数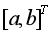列代入白化微分方程，以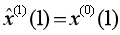为初始条件求出一阶累加序列的预测公式（4），一阶累减生成原始序列的预测公式（5）。因此，GM(1,1)模型的预测精度取决于：（1）参数列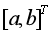的估计精度，显然，参数列通过差分方程传递给白化微分方程，为进一步探究定义式与白化微分方程之间的关系，将微分方程（3）两边同时从k-1到k积分，得 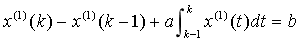，与GM(1,1)模型定义式相比可知，准确的背景值应为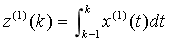，几何意义为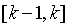区间内曲线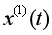到横坐标轴间的积分面积，而传统模型中以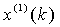和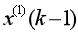的均值取代了准确背景值。由此可知, 背景值构造形式的偏差通过参数列的估计影响模型拟合误差精度，形成建模系统的误差估计精度；（2）灰色微分方程模型初始条件的选取，传统GM(1,1)模型取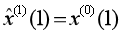作为初始值，这就假定拟合曲线必定过点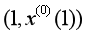，当实际初始值偏离整体规律时，得到的模型也会偏离整体规律，进而影响模型精度，因此初始值的选取至关重要。基于以上分析可知，同时优化背景值和初始条件能够有效提升模型的预测精度。

2 GM(1,1)模型优化

2.1背景值优化  

定理 1 ，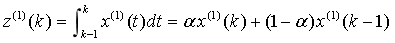

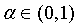
证明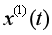：为单调递增序列，由第二积分中值定理可知，  

，

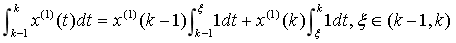令

在最小二乘意义下，参数列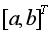的估计值为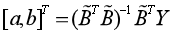：。在传统GM(1,1)模型中，通常取背景值系数。从定积分几何的意义上来看，传统模型用梯形面积取代了曲面梯形面积，当累加函数增速较快时，产生的误差越大，这也是传统GM(1,1)模型在发展系数-a大于3时拟合误差逐渐增大主要原因。显然a的选取与一阶累加序列曲线形式密切相关，为提升拟合精度，a的取值应根据序列的性质确定。  

2.2 初始值优化

定理2   相对平均误差平方和最小准则下，时间响应式常数C最优与初始条件最优等价。

证明： （1）时间响应式常数C最优

2.3 背景值系数a的确定

注意到模型为非线性优化问题，借助非线性无约束优化模型，利用 LINGO、MATLAB 等软件或者智能算法（粒子群、遗传算法等）可以实现对背景值系数a的最优化求解。本文采用智能算法中的粒子群优化算法 (PSO)确定最优参数^[10-11]。

3 实例分析

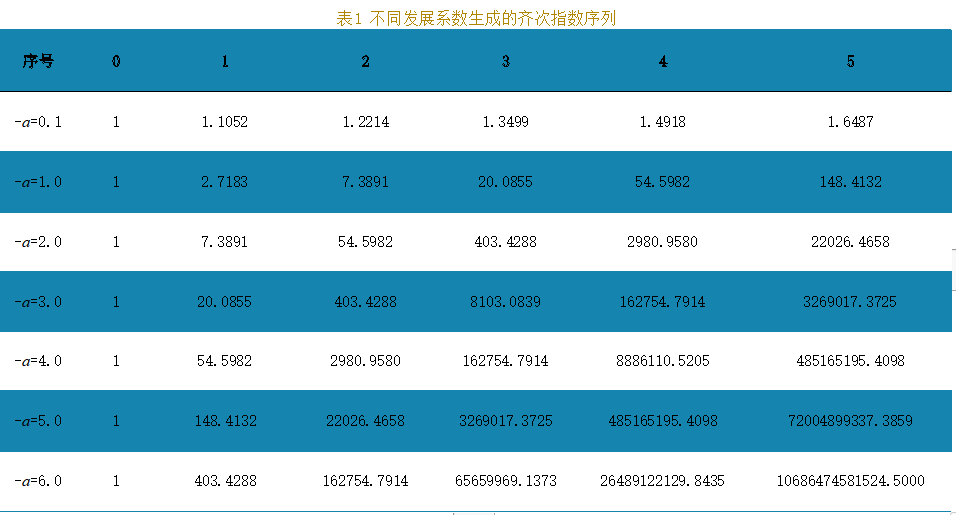
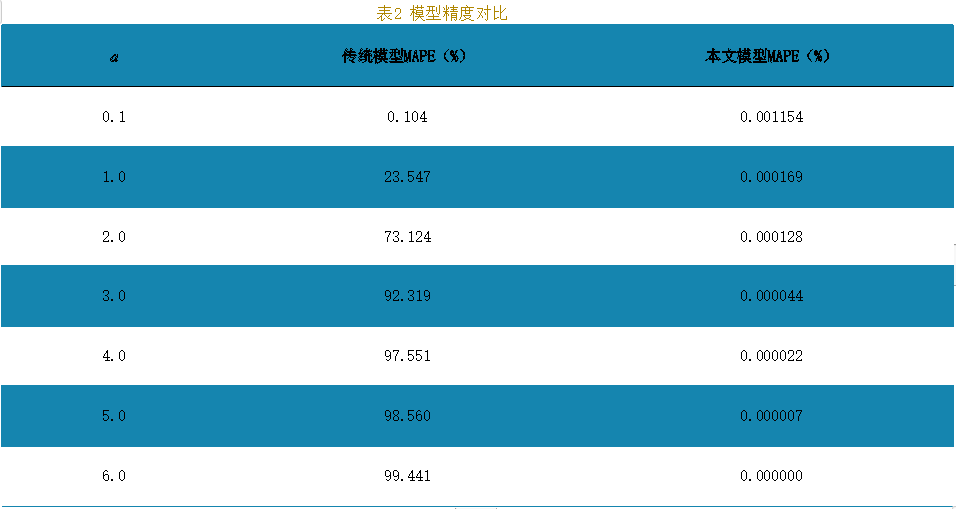
由表2可知，传统GM(1,1)模型误差随着发展系数的增大迅速增加，新的模型精度均高于99%，且随着发展系数增加，误差不断减少，这说明模型能够高度拟合齐次指数增长序列。

在实际应用方面，选取2017~2021年我国新能源汽车保有量（见表3）为原始序列进行预测，将本文模型的预测结果分别与传统模型（模型一）、文献[6]提出的基于误差最小化的背景值优化GM(1,1)预测模型（模型二）和文献[9]提出的对初值条件及背景值进行综合优化的预测模型（模型三）进行对比（见表4）。

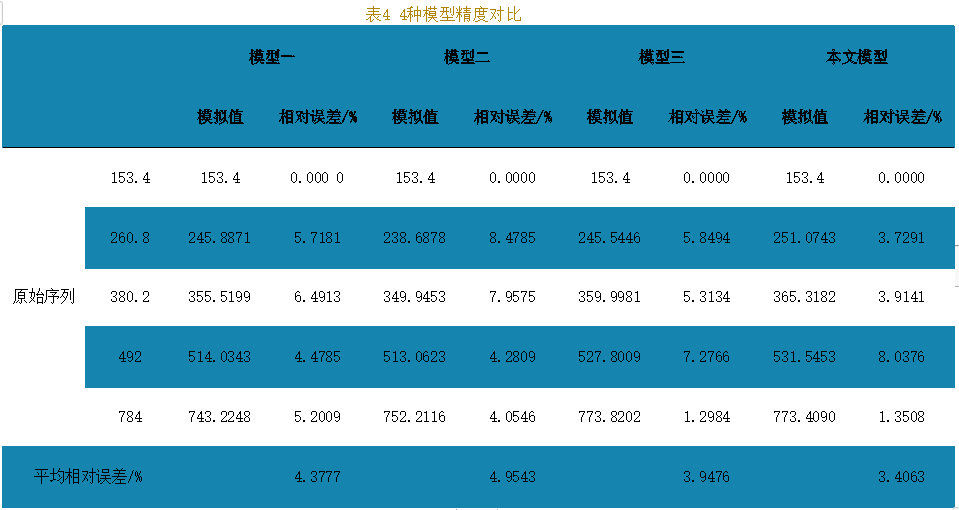
从表4中4种模型的模拟值、相对误差以及平均相对误差可知，模型一、模型二、模型三所得模拟数据的平均相对误差分别为4.3777%、4.9543%、3.9476%，模型的平均相对误差为 3.4036%，综合优化模型的预测精度优于其他模型。

4 结语

采用平均相对误差最小准则，构建适应度函数，结合粒子群算法动态有效寻优的特性，实现了传统GM(1,1)模型的背景值系数和初始值同时优化。通过对齐次指数序列的模拟分析可知，当发展系数α接近6时，接近完全拟合，这说明提出的模型可用于中长期预测，其适用范围较传统GM(1,1)模型有了较大的扩展。实例验证可知，该模型在预测精度上优于已有的背景值和初始条件综合优化的GM(1,1)模型。

参考文献

[1] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.

[2] 蒋诗泉,刘思峰,周兴才.基于复化梯形公式的GM(1,1)模型背景值的优化[J].控制与决策,2014,29(12):2221-2225.

[3] 王晓佳,杨善林.基于组合插值的模型预测方法的改进与应用[J].中国管理科学,2012,20(2):129-134.

[4] 张可,刘思峰.基于粒子群优化算法的广义累加灰色模型[J].系统工程与电子技术,2010,7(32):1437-1440.

[5] 杨孝良,周猛,曾波.灰色预测模型背景值构造的新方法[J].统计与决策,2018,(19):14-17.

[6] 徐宁,党耀国,丁松.基于误差最小化的GM(1,1)模型背景值优化方法[J].控制与决策,2015,30(2):283-288.

[7] 熊萍萍,党耀国,姚天祥.基于初始条件优化的一种非等间距 GM(1,1)建模方法[J].控制与决策,2015,30(11):2097-2102.

[8] 张彬,西桂权.基于背景值和边值修正的GM(1,1)模型优化[J].系统工程理论与实践,2013,33(3):682-688.

[9] 郑雪平,王大国,水庆象.基于背景值和初始条件综合优化的GM(1,1)预测模型[J].统计与决策,2021,(9):25-28.

[10] 王亮,滕克难,吕卫民,等.基于粒子群算法的非线性时变参数离散灰色预测模型[J].统计与决策,2015,(12):16-19.

[11] 于丽亚,王丰效.基于粒子群算法的非等距GOM(1,1)模型[J].纯粹数学与应用数学,2011,27(4):472-475.

Optimization of GM(1,1) Model Based on Particle Swarm Algorithm

WANG Luxin

(Basic teaching department, Jiangsu Shipping College, Nantong  Jiangsu  226010)

Abstract:GM (1, 1) model is a gray index model with a wide range of applications, and its accuracy depends on the structure of the background value and the selection of initial conditions. The article proposes a GM (1, 1) model based on the particle swarm algorithm to optimize the background value coefficients and initial conditions under the error minimization criterion. The optimized model is used to fit the sub-index sequence, the number of new energy cars of China from 2017 to 2021 , and the wind power generation of China from 2012 to 2020. The example analysis shows that the new optimized GM (1, 1) model is suitable for medium and long-term prediction and also has higher accuracy.

Key words:GM(1,1) model;particle swarm optimization;background value;initial condition;error minimization